On va ici aborder une partie fondamentale du tableur, car elle introduit le domaine de la logique.
En mathématique, il existe une notion importante que l’on nomme Albègre de Boole.
Cette branche des mathématiques s’intéresse à une approche algébrique de la logique.
Elle fut lancée en 1854 par le mathématicien britannique George Boole.
Aujourd’hui, elle trouve de nombreuses applications en informatique et dans la conception des circuits électroniques.
Le principe général
On utilise des valeurs binaires, c’est-à-dire 0 et 1, pour représenter la vérité (vrai ou faux, oui ou non, tout ou rien).
Voyez cela comme les interrupteurs de lumière : ils peuvent être en position « on » (1, vrai) ou « off » (0, faux).
On a donc des variables qui peuvent prendre 2 états :
- Vrai → 1
- Faux → 0
On a trois opérations principales dans cette algèbre :
- le ET (AND)
- le OU (OR)
- le NON (NOT)
Les tables de vérité
Dans cette algèbre, une notion primordiale, c’est la table de vérité.
Une table de vérité est un tableau qui montre toutes les possibilités de valeurs pour des variables et le résultat des opérations entre elles.
C’est comme si on faisait un tableau pour résumer tous les résultats possibles d’un jeu de questions-réponses.
La fonction ET
On parle ici de table de vérité, de conjonction.
L’opération ET donne un résultat “vrai” seulement si toutes les conditions sont vraies. Sinon, le résultat est “faux”.
Partons d’un exemple simple :
- A : « Il fait jour. »
- B : « Il pleut. »
Pour que l’affirmation :
« Il fait jour ET il pleut » soit vraie, il faut que les deux conditions soient remplies en même temps.
Voici sa table de vérité :
| A (Il fait jour) | B (Il pleut) | A ET B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Pour le tableur, si nous avons le tableau suivant :
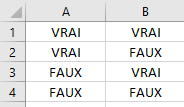
Pour que la valeur soit vraie, les 2 cellules doivent avoir la valeur VRAI
Soit le résultat en colonne C
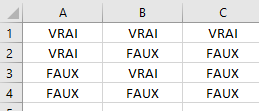
Son écriture sera la suivante :
=ET(A1;B1)Cas pratique
On a le tableau suivant
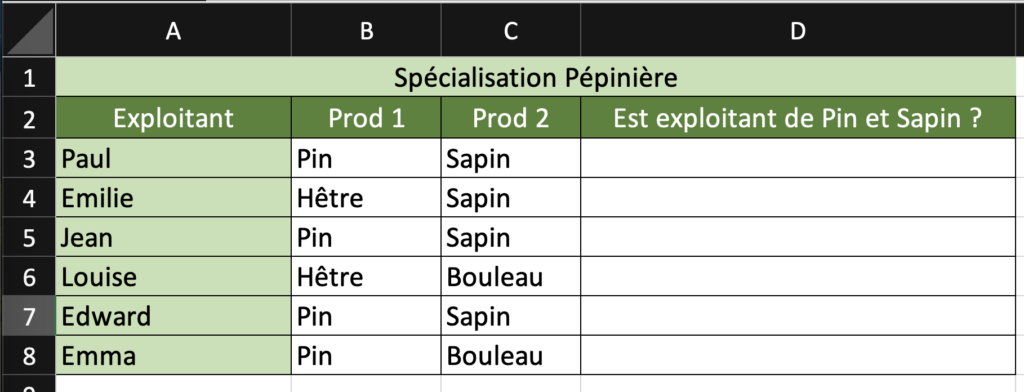
On va renseigner nos critères :
- Ici le vrai doit être Pin, mais aussi Sapin
- On va donc écrire : B3=”Pin” car on vérifie l’information Pin dans cette cellule.
- De même, on va écrire : C3=”Sapin” afin de vérifier que l’information Sapin est dans cette cellule.

La formule :
=ET(B3="Pin";C3="Sapin")
Le résultat final est donc :
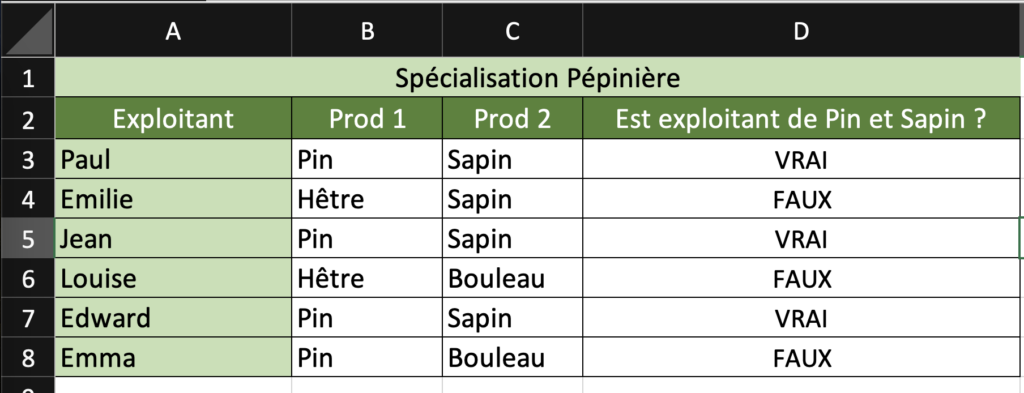
La fonction OU
On parle ici de table de vérité, de disjonction.
L’opération OU est “vraie” si au moins une des conditions est vraie.
Reprenons notre exemple :
Pour l’affirmation « Il fait jour OU il pleut », il suffit qu’une des deux conditions (ou les deux) soit vraie pour que le résultat soit vrai.
Voici la table de vérité pour OU :
| A (Il fait jour) | B (Il pleut) | A OU B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Pour le tableur, si nous avons le tableau de l’exemple précédent :

Pour que la valeur soit vraie, l’une des deux cellules doit avoir la valeur VRAI
Soit le résultat en colonne C
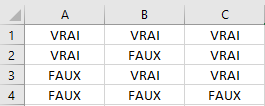
Son écriture sera la suivante :
Cas pratique
=OU(A1;B1)On a le tableau suivant
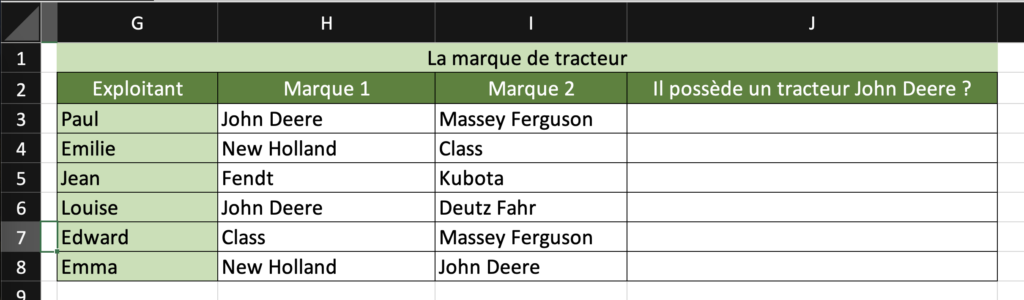
On va renseigner nos critères :
- Ici le vrai doit être John Deere
- On va donc écrire : H3=”John Deere” car on vérifie l’information John Deere dans cette cellule.
- Mais on va aussi écrire : I3=”John Deere” afin de vérifier que l’information John Deere est dans cette cellule.

La formule :
=OU(H3="John Deere";I3="John Deere")
Le résultat final est donc :
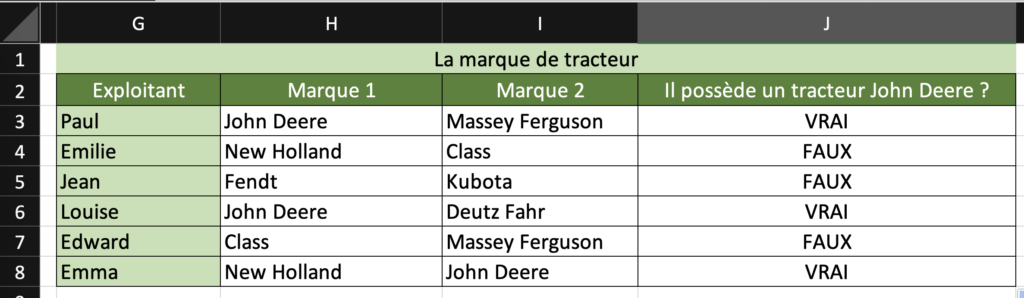
La fonction NON
On parle ici de négation. Cette opération est un peu spéciale par rapport au ET et au OU que nous avons vu juste avant.
Alors que ET et OU travaillent avec deux variables à la fois, NON s’applique à une seule variable.
Elle inverse l’état de cette variable : si la variable est vraie (1), NON la rend fausse (0), et si elle est fausse (0), NON la rend vraie (1).
C’est comme un interrupteur qui change toujours de position, peu importe son état initial.
La table de vérité pour l’opération NON est alors très simple puisqu’elle n’implique qu’une seule variable.
Disons que nous avons une affirmation A : « Il fait jour.”
| A (Il fait jour) | NON A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Dans cette table, vous pouvez voir que si « Il fait jour » est faux (0), alors « Il NE fait PAS jour » (NON A) est vrai (1).
Et si « Il fait jour » est vrai (1), alors « Il NE fait PAS jour » (NON A) est faux (0).
En résumé :
La fonction NON, permet de renvoyer la valeur contraire.
Elle inverse la valeur logique de l’argument :
- Renvoie FAUX pour un argument VRAI
- Renvoie VRAI pour un argument FAUX
Son écriture est la suivante :
Exemple Si dans une cellule A1, j’ai la valeur VRAI, je vais écrire la formule suivante :
=NON(A1="VRAI")Exemple concret :
Vous avez une liste de tâches avec une colonne qui indique si elles sont « Terminées » ou non. Dans la colonne A, vous avez les tâches, et dans la colonne B, un « 1 » si la tâche est terminée (vrai), et « 0 » si elle ne l’est pas (faux).
| A | B |
|---|---|
| Plantations | 1 |
| Arrosage | 0 |
| Nettoyage | 1 |
Si vous voulez savoir quelles tâches ne sont pas terminées en utilisant l’opération NON, vous pouvez créer une formule dans une nouvelle colonne.
Notre formule serait alors :
=NON(B2)Cela convertira le « 1 » (vrai) en FAUX, et le « 0 » (faux) en VRAI, car NON inverse la valeur.
Le tableau serait donc le suivant :
| A | B (Terminée) | C (NON Terminée) |
|---|---|---|
| Plantations | 1 | FAUX |
| Arrosage | 0 | VRAI |
| Nettoyage | 1 | FAUX |
La colonne C utilise l’opération NON pour indiquer les tâches qui ne sont pas terminées.
- Si B est « 1 » (ce qui signifie que la tâche est terminée), C deviendra « FAUX » parce que NON(B) inverse la valeur de B.
- Si B est « 0 » (la tâche n’est pas terminée), alors C affichera « VRAI », indiquant que la tâche n’est effectivement pas terminée selon la logique NON.


